При работе с пределами встречаются выражения, в которых числитель и знаменатель ведут себя непредсказуемо и создают неопределённость. В таких ситуациях техника дифференцирования помогает разложить сложную дробь на понятные шаги, поэтому правило Лопиталя простыми словами воспринимается как способ удобнее рассмотреть структуру выражения. Когда возникает необходимость понять, что такое правило Лопиталя, внимание сосредотачивается на том, как производные влияют на поведение дроби и делают вычисления более прозрачными.
Сущность метода и условия применения
Правило Лопиталя это приём, который применяют к пределам дробей, если числитель и знаменатель одновременно стремятся к нулю или бесконечности. Так возникает неопределённость, требующая специального подхода. Чтобы понять, когда используется правило Лопиталя, нужно учитывать непрерывность функций, наличие производных и поведение выражения вблизи точки. При выполнении этих условий правило Лопиталя формула позволяет вычислить предел, заменив обе части дроби их производными. В результате получают выражение, которое легче упорядочить.
Основные обозначения
При работе с пределами и производными используют несколько стандартных обозначений, без которых невозможно корректно применять метод. Пределы записывают в виде lim (x → a) f(x), где указано, к какой точке стремится переменная. Производные обозначают как f′(x) или df/dx, что позволяет сразу видеть, какая функция дифференцируется. В дробях, где появляется неопределённость, важно точно определить форму выражения — например, 0/0 или ∞/∞, потому что именно эти типы позволяют применять метод. Такие обозначения помогают проследить, как меняется структура выражения на каждом этапе.
Формулировка метода
Чтобы применить правило Лопиталя формула, сначала проверяют форму дроби. Если числитель и знаменатель стремятся к нулю или бесконечности, обе функции дифференцируют отдельно. После этого предел вычисляют для новой дроби, состоящей из производных.
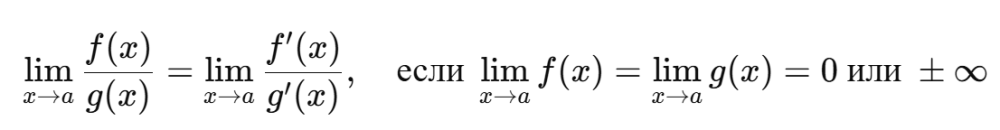
Такая замена уменьшает сложность выражения, потому что производные часто имеют более простую структуру или устойчивое поведение вблизи точки. Если после первого дифференцирования сохраняется неопределённость, процесс повторяют, пока выражение не приобретёт чёткую форму. Так выглядит полный механизм применения метода в учебных примерах.
Логика и обоснование
В курсах анализа приводят правило Лопиталя доказательство, в котором объясняется корректность перехода от исходных выражений к производным. Это основано на свойствах непрерывных функций и поведении выражений в малых окрестностях точки, где возникает неопределённость. Такой подход объединяет практическую и теоретическую части метода.
Практическая часть и разбор типичных ситуаций
Удобнее всего начинать с простых выражений, в которых обе части дроби образуют форму 0/0. В таких случаях хорошо видно использование правила Лопиталя, потому что после дифференцирования структура примера упрощается. В тригонометрических, логарифмических и экспоненциальных выражениях принцип остаётся тем же, поэтому нахождение пределов по правилу Лопиталя постепенно становится понятным инструментом. Важно сохранять последовательность действий, потому что она влияет на точность результата.
Вычисление разных типов выражений
В более сложных задачах вычисление пределов по правилу Лопиталя предполагает повторное дифференцирование, если появляется новая неопределённость. В результате дробь приобретает более простой вид, а преобразования становятся логичнее. Это показывает практическую пользу метода при работе с большими или сложными выражениями.
Типичные ошибки
В работе с методом встречаются повторяющиеся неточности, которые влияют на результат и требуют внимания на каждом этапе преобразований. Наиболее распространённые среди них:
- неверная форма;
- пропуск производной;
- преждевременное сокращение;
- смешивание типов;
- игнорирование условий;
- лишнее повторение.
Задания и тренировочные примеры
В учебном процессе важно разбирать разные категории выражений, потому что это помогает увидеть, как меняется структура дроби после дифференцирования. Задания на правило Лопиталя позволяют отработать последовательность действий без лишних преобразований. В примерах, где требуется найти предел используя правило Лопиталя, заметно, как производные упрощают выражение и формируют итоговый результат.
Пример 1.
Вычислить предел:
lim (x → 0) (sin x) / x
После дифференцирования числителя и знаменателя получаем cos x / 1. Предел равен 1.
Пример 2.
Вычислить предел:
lim (x → ∞) (ln x) / x
Производные дают (1/x) / 1. Предел стремится к 0, поэтому выражение убывает без дополнительных преобразований.
Пример 3.
Вычислить предел:
lim (x → 0) (e^x − 1 − x) / x²
Требуются два последовательных дифференцирования. После них получаем e^x / 2, поэтому предел равен 1/2.Типичные категории, охватывающие основные виды заданий:
- базовые выражения;
- сложные дроби;
- тригонометрические пределы;
- экспоненциальные функции;
- логарифмические примеры;
- комбинированные случаи.
| Ситуация | Можно применять | Пояснение |
| 0/0 | да | переход к производным упрощает структуру выражения |
| ∞/∞ | да | дифференцирование снижает темп роста функций |
| другие формы | нет | нужны дополнительные преобразования |

Метод позволяет упорядочить выражения, в которых поведение дроби усложняет вычисление предела. Переход к производным помогает увидеть логику изменений и получить результат в последовательной и понятной форме.