Під час роботи з межами трапляються вирази, у яких чисельник і знаменник поводяться непередбачувано й створюють невизначеність. У таких ситуаціях техніка диференціювання допомагає розкласти складний дріб на зрозумілі кроки, тому правило Лопіталя простими словами сприймається як спосіб подивитися на структуру виразу зручніше. Коли виникає потреба з’ясувати, що таке правило Лопіталя, увага зосереджується на тому, як похідні впливають на поведінку дробу та роблять обчислення прозорішими.
Сутність методу та умови застосування
Правило Лопіталя це прийом, який застосовують до меж дробів, якщо чисельник і знаменник одночасно прямують до нуля або нескінченності. Так утворюється невизначеність, що потребує спеціального підходу. Щоб зрозуміти, коли використовується правило Лопіталя, потрібно враховувати неперервність функцій, наявність похідних та аналіз поведінки виразу поблизу точки. За виконання цих умов правило Лопіталя формула дозволяє обчислити межу, замінивши обидві частини дробу їхніми похідними. У результаті отримують вираз, який легше впорядкувати.
Основні позначення
Під час роботи з межами та похідними використовують кілька стандартних позначень, без яких неможливо коректно застосувати метод. Границі записують у вигляді lim (x → a) f(x), де показано, до якої точки прямує змінна. Похідні позначають як f′(x) або df/dx, що дає змогу одразу бачити, яка функція диференціюється. У дробах, де з’являється невизначеність, важливо точно визначити форму виразу – наприклад, 0/0 або ∞/∞, бо саме ці типи дозволяють застосовувати метод. Завдяки таким позначенням легко простежити, як змінюється структура виразу на кожному етапі.
Формулювання методу
Щоб застосувати правило Лопіталя формула, спершу перевіряють форму дробу. Якщо чисельник і знаменник наближаються до нуля або нескінченності, обидві функції диференціюють окремо. Після цього межу обчислюють для нового дробу, який складається з похідних.
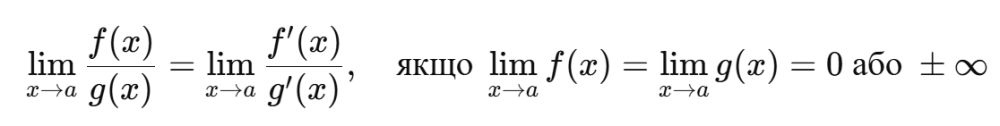
Така заміна дає можливість зменшити складність виразу, бо похідні часто мають простішу структуру або стабільнішу поведінку біля точки. Якщо після першого диференціювання залишається невизначеність, процес можна повторювати, доки вираз не набуде чіткої форми. Це і є повна механіка застосування методу, яка використовується в навчальних прикладах.
Логіка та обґрунтування
У курсах аналізу подають правило Лопіталя доведення, у якому пояснюється коректність переходу від початкових виразів до похідних. Це спирається на властивості неперервних функцій та поведінку виразів у малих околах точки, де виникає невизначеність. Такий підхід поєднує практичний і теоретичний аспекти методу.
Практична частина та розбір типових ситуацій
Найзручніше починати з простих виразів, у яких обидві частини дробу утворюють форму 0/0. У таких випадках добре видно використання правила Лопіталя, бо після диференціювання структура прикладу спрощується. У тригонометричних, логарифмічних і експоненційних виразах принцип залишається таким самим, тому знаходження границь за правилом Лопіталя поступово стає зрозумілим інструментом. Важливо зберігати послідовність кроків, бо вона впливає на правильність кінцевого результату.
Обчислення різних типів виразів
У складніших завданнях обчислення границь за правилом Лопіталя передбачає повторне диференціювання, якщо з’являється нова невизначеність. У результаті дріб набуває простішого вигляду, а перетворення стають логічнішими. Це демонструє практичну користь методу, коли потрібно опрацювати великі або складні вирази.
Типові помилки
У роботі з методом трапляються повторювані неточності, які впливають на результат і потребують уважності під час кожного кроку перетворень. Найпоширені серед них такі:
- невірна форма;
- пропуск похідної;
- передчасне скорочення;
- змішування типів;
- ігнорування умов;
- зайве повторення.
Завдання та тренувальні приклади
У навчальному процесі важливо опрацьовувати різні категорії виразів, бо це допомагає побачити, як змінюється структура дробу після диференціювання. Завдання на правило Лопіталя дозволяють відпрацювати послідовність дій без зайвих кроків. У вправах, де потрібно знайти границі використовуючи правило Лопітеля, добре видно, як похідні впливають на спрощення та формування кінцевого результату.
Приклад 1.
Обчислити межу:
lim (x → 0) (sin x) / x
Після диференціювання чисельника й знаменника отримуємо cos x / 1. Межа дорівнює 1.
Приклад 2.
Обчислити межу:
lim (x → ∞) (ln x) / x
Похідні дають (1/x) / 1. Межа прямує до 0, тому вираз зменшується без додаткових перетворень.
Приклад 3.
Обчислити межу:
lim (x → 0) (e^x − 1 − x) / x²
Потрібні два послідовні диференціювання. Після них отримуємо e^x / 2, тому межа дорівнює 1/2.Типові категорії, що охоплюють основні види завдань:
- базові вирази;
- складні дроби;
- тригонометричні межі;
- експоненційні функції;
- логарифмічні приклади;
- комбіновані випадки.
| Ситуація | Можна застосовувати | Пояснення |
| 0/0 | так | перехід до похідних спрощує структуру виразу |
| ∞/∞ | так | диференціювання зменшує темп зростання функцій |
| інші форми | ні | потрібні додаткові перетворення |

Метод дає змогу впорядкувати вирази, у яких поведінка дробу ускладнює обчислення межі. Перехід до похідних допомагає побачити логіку змін у виразі та отримати результат у послідовній і зрозумілій формі.















